Journal of Applied Mathematics and Physics
Vol.04 No.04(2016), Article ID:65980,4 pages
10.4236/jamp.2016.44086
Non-Negative Integer Solutions of Two Diophantine Equations 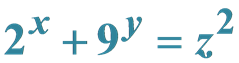 and
and 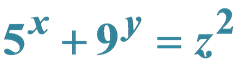
Md. Al-Amin Khan, Abdur Rashid, Md. Sharif Uddin
Department of Mathematics, Jahangirnagar University, Dhaka, Bangladesh

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).



Received 7 October 2015; accepted 24 April 2016; published 27 April 2016
ABSTRACT
In this paper, we study two Diophantine equations of the type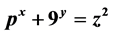 , where p is a prime number. We find that the equation
, where p is a prime number. We find that the equation 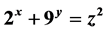 has exactly two solutions
has exactly two solutions 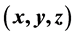 in non-negative integer i.e.,
in non-negative integer i.e., 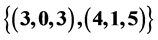 but
but 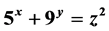 has no non-negative integer solution.
has no non-negative integer solution.
Keywords:
Exponential Diophantine Equation, Integer Solutions

1. Introduction
Recently, there have been a lot of studies about the Diophantine equation of the type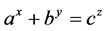 . In 2012, B. Sroysang [1] proved that
. In 2012, B. Sroysang [1] proved that 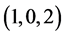 is a unique solution
is a unique solution 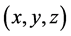 for the Diophantine equation
for the Diophantine equation 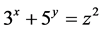 where
where 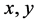 and z are non-negative integers. In 2013, B. Sroysang [2] showed that the Diophantine equation
and z are non-negative integers. In 2013, B. Sroysang [2] showed that the Diophantine equation  has a unique non-negative integer solution
has a unique non-negative integer solution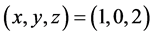 . In the same year, B. Sroysang [3] found all the solutions to the Diophantine equation
. In the same year, B. Sroysang [3] found all the solutions to the Diophantine equation 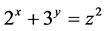 where
where 










In this study, we consider the Diophantine equation of the type 


2. Main Results
Theorem 2.1. (Catalan’s Conjecture [12] ) The Diophantine equation



Theorem 2.2. The Diophantine equation 

Proof: Let x and z be non-negative integers such that









Case-1: If







Case-2: If



Hence, 

Theorem 2.3. The Diophantine equation

Proof: Let x and z be non-negative integers such that





or
Let 



or
Thus, 





Therefore, 

Corollary 2.4. The Diophantine equation 
Theorem 2.5. The Diophantine equation 
Proof: Suppose x and z be non-negative integers such that









or
Thus, 




Theorem 2.6. The Diophantine equation 


Proof: Suppose 










Now we consider the following remaining cases.
Case-1:



and




Case-2:
















Case-3:


Case-4:


Let 









The Diophantine Equation (1) is a Diophantine equation by Catalan’s type 


Theorem 2.7. The Diophantine equation 
Proof: Suppose 






Now we consider the following remaining cases.
Case-1:













Case-2:












Case-3:


Case-4:

Let 












3. Conclusion
In the paper, we have discussed two Diophantine equation of the type




Cite this paper
Md. Al-Amin Khan,Abdur Rashid,Md. Sharif Uddin, (2016) Non-Negative Integer Solutions of Two Diophantine Equations 2x + 9y = z2 and 5x + 9y = z2. Journal of Applied Mathematics and Physics,04,762-765. doi: 10.4236/jamp.2016.44086
References
- 1. Sroysang, B. (2012) On the Diophantine Equation . International Journal of Pure and Applied Mathematics, 81, 605-608.
- 2. Sroysang, B. (2013) On the Diophantine Equation . International Journal of Pure and Applied Mathematics, 89, 111-114.
- 3. Sroysang, B. (2013) More on the Diophantine Equation . International Journal of Pure and Applied Mathematics, 84, 133-137.
http://dx.doi.org/10.12732/ijpam.v84i2.11 - 4. Rabago, J.F.T. (2013) On Two Diophantine Equations and . International Journal of Computing Science and Mathematics, 3, 28-29.
- 5. Acu, D. (2007) On a Diophantine Equation . General Math, 15, 145-148.
- 6. Chotchaisthit, S. (2012) On the Diophantine Equation Where p Is a Prime Number. American Journal of Mathematical and Management Sciences, 1, 191-193.
- 7. Mihailescu, P. (2004) Primary Cycolotomic Units and a Proof of Catalan’s Conjecture. Journal für die Reine und Angewandte Mathematik, 27, 167-195.
- 8. Suvarnamani, A. (2011) Solutions of the Diophantine Equation . International Journal of Mathematical Sciences and Applications, 1, 1415-1419.
- 9. Suvarnamani, A., Singta, A. and Chotchaisthit, S. (2011) On Two Diophantine Equations and . Science and Technology RMUTT Journal, 1, 25-28.
- 10. Rabago, J.F.T. (2013) More on the Diophantine Equation of Type . International Journal of Computing Science and Mathematics, 3, 15-16.
- 11. Sroysang, B. (2012) More on the Diophantine Equation . International Journal of Pure and Applied Mathematics, 81, 601-604.
- 12. Catalan, E. (1844) Note Extraite Dune Lettre Adressee a Lediteur. Journal für die Reine und Angewandte Mathematik, 27, 192.
http://dx.doi.org/10.1515/crll.1844.27.192






